2018 SCUPC 校赛D题

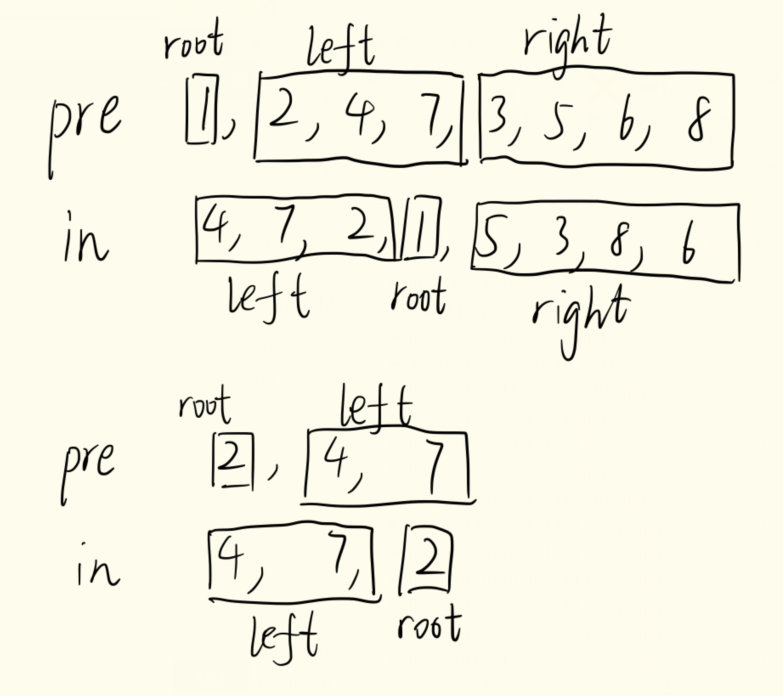
2018校赛中的D题是除了两道签到题之外AC数最多的一题，然而我却感觉这题的难度在蓝桥杯初赛里面可以算压轴了吧。这也是我唯做出来的一题，大佬们打扰了。
下面来回顾一下这道AC数最多的非签到题。

Description
在自然数序列(0,1,2,3,4,5…)中,求去掉所有含2,3,5,7的数字后(0,1,4,6,8,9…)的第k个数.

Input
第1行为输入组数T。
第2—T+1行为长度k。
T≤1000,1≤k≤1000000000000

Output
每组样例输出一行。

Sample Input
3
1
4
1000000000000

Sample Output
0
6
4086441010601686

Time Limit: 1000ms, Memeory Limit: 64MB

第一次打这种真格算法竞赛的我，第一次想的是直接枚举暴力（来自暴力蓝桥杯省二选手的挣扎），然后队友告诉我1000000000以上枚举一遍直接超时，果然我还是不懂规矩啊TAT。
那怎么办呢？找规律吧，不如先把0到100满足条件的数列出来再看看？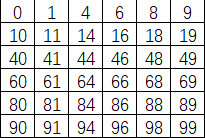

可以看到前10个自然数[0,9]中满足条件的有6个数，前100个自然数[0,99]中满足条件的有36个数，所以可以大胆地猜测，前10的n次方个自然数中有6的n次方个是满足条件的。（这是当时解题时的思路，然而好像这个思路对解题影响并不大）
现在我们知道98这个自然数是第35个满足条件的自然数。那逆过来是怎么推导的呢？
上面的矩阵一行是6个数，所以第35个数应该是在第（35//6+1）行，第(35mod6)列，也就是6行5列。
那6行5列和98有关系吗？其实把上面的矩阵换个方法看，可以变成这样：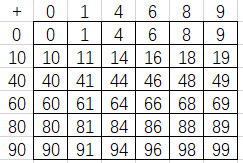

看看行标和列标可以说6行5列是90+8=9*10+8*1
我们建立一个映射

F(a) = {1,2,3,4,5,6}->{0,1,4,6,8,9}

那么

98==F(6)*10+F(5)*1==9*10+8*1

到了这里问题已经很明显了，这是一道进制转换的数论题，要求把十进制减一（这里要注意0占了一个坑）转换成六进制，再对这个6进制数每一位进行一次映射。进制转换的问题，用短除法就可以解决，至于映射，写一个数组就好了。

Code

#include<iostream>
using namespace std;

long long int pow(int i, int n) { //重复造轮子症
	if(n == 0)
		return 1;
	if(n == 1)
		return i;
	return i * pow(i, n-1);
}

int main() {
	int map[6] = {0,1,4,6,8,9}; //用于映射的数组 
	int t;
	cin >> t;
	for(int i = 0; i < t; i++) {
		long long int tmp, sum = 0;
		int len = 0;
		cin >> tmp;
		long long int k = tmp - 1;
		while(k != 0) { //短除法 
			int bit = k % 6;
			sum += pow(10, len) * map[bit];
			len++;
			k /= 6;
		}
		cout << sum << endl;
	}
	return 0;
}

不得不说这道AC数最高的题花了我两个小时的时间。