题目描述

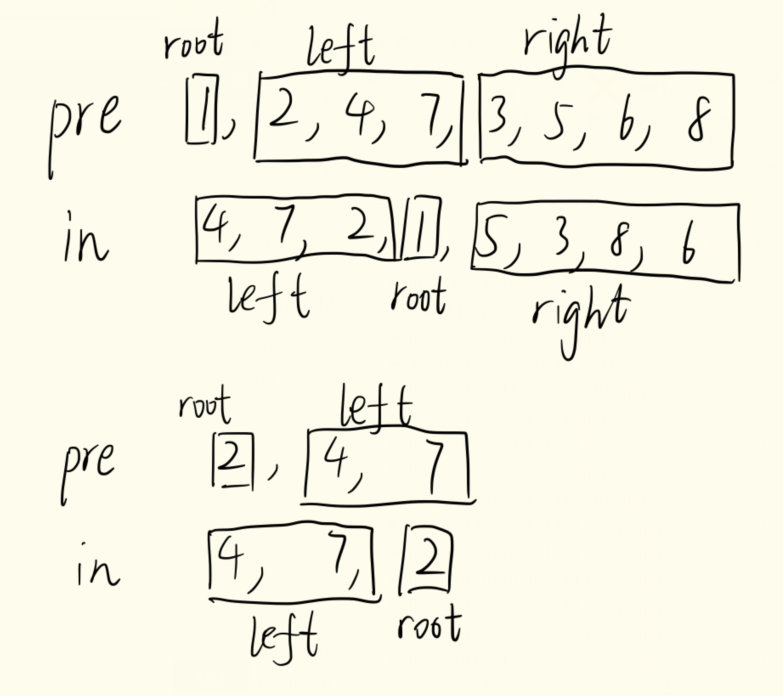
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解题思路

这道题是大二数据结构课程的期末考试题，当时是手算，现在需要用代码实现。
解题算法如下：在前序遍历序列中取出第一个数，在中序遍历序列中找到它的下标，那么就把这个数作为根节点，它的左子树的中序遍历序列就在这个数的左边，左子树的前序遍历序列元素个数与中序遍历相同，剩下的数就是右子树的序列。把左右子树的序列进行相同的操作，递归下去就可以得到它们的结构。再把左右子树与根节点连接起来，就可以得到目标树。

定义Tree(pre, in, preStart, preEnd, inStart, inEnd)为一颗子树
其中pre[preStart: preEnd]为这颗子树的前序遍历序列，
in[inStart: inEnd]为这颗子树的中序遍历序列。

设i为这颗子树根节点在整个中序遍历序列中的下标
那么它左子树的前序遍历序列为pre[preStart+1: preStart+i-inStart]，
中序遍历序列为in[inStart: i-1]；
右子树的前序遍历序列为pre[preStart+i-inStart+1: preEnd]，
中序遍历序列为in[i+1: inEnd]。
（这里比较难推，画图思考一下）

题解（带注释）

java

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
import java.util.*;

public class Solution {
    private Map<Integer, Integer> indexMap;

    private TreeNode reconstructHelp(int[] pre, int[] in, int preStart, int preEnd, int inStart, int inEnd) {
        // 首先判断这颗子树是不是不应该存在，显然前指针超越后指针时，这棵树不存在
        if(preStart > preEnd || inStart > inEnd)
            return null;
        // 获取当前根节点在中序遍历序列中的下标
        int targetIndex = indexMap.get(pre[preStart]);
        TreeNode root = new TreeNode(pre[preStart]);
        // 根据上面的递推关系得到左右子树
        TreeNode left = reconstructHelp(pre, in, preStart+1, preStart+targetIndex-inStart, inStart, targetIndex-1);
        TreeNode right = reconstructHelp(pre, in, preStart+targetIndex-inStart+1, preEnd, targetIndex+1, inEnd);
        // 最后将左右子树连接至当前的根节点
        root.left = left;
        root.right = right;
        return root;
    }

    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        indexMap = new HashMap();
        // 由于数字没有重复，所以可以对in列表进行下标反向索引，避免查找
        for(int i = 0; i < in.length; i++)
            indexMap.put(in[i], i); //反向索引
        TreeNode result = reconstructHelp(pre, in, 0, pre.length-1, 0, in.length-1);
        return result;
    }
}